Programming P-adic Numbers
Number theorists tend to emphasize the algebraic side and to focus on results that show up in their work. Calculate next digit of p-adic number rem ModP self.
Infinite Primes PART II.

Programming p-adic numbers. Completions of the rationals. These include a library for p-adic numbers and several functions on infinite lists and -terms. NUMBER THEORETICAL VISION TGD as a Generalized Number Theory I.
Numbers with more ps are smaller. Any p-adic number xcan be represented as a series x ik a ip. Quaternions Octonions and their Hyper CounterpartsTGD as a Generalized Number Theory III.
P-adic Langlands programme p-adic Hodge theory GL 2Q p -modules completed cohomology. The p-adic numbers expression through the use of this in nite series is called a p-adic expansion. However I felt that her very-first mention and definition of the p-adic norm p.
Further insight into mysteries of values of zeta functions at integers joint with Jan Minac. For example in the 3-adics 486 is small because it has many 3s in its prime factorization 486. Just as 1300 on a 24-hour clock is the same as 1 pm mathematicians say that 13 modulo 12 is equivalent to 1.
Let 6 pbe another prime number and Q an algebraic closure of Q. The completion is the set of p-adic numbers. They also allow us to use methods from calculus and analysis to obtain results in algebra and number theory.
TGD P-ADIC NUMBERS AND ADELES. The local-global principle functions defined by power series p-adic interpolation p-adic measures. So we may identify the rationals in the p-adic numbers and thus consider elements in the completion that are not in the rationals to be irrational p-adic numbers.
The Nemo code written in Julia is licensed under the BSD license and it makes use of GPL andLGPL CC libraries such as. P-adic Γ-function 67 p-adic integers 33 p-adic interpolation 65 p-adic Weierstrass preparation the-orem 159 161 p-adic distribution 103 p-adic regulator 130 ABC conjecture 5 Adams congruences 22 Ankeny 120 127 Artin 120 127 Artin-Hasse exponential 40 Aryabhata 11 Bernoulli distribution 105 Bernoulli numbers 2 11. __init__ self p self.
Functions such as sqrt log exp sin cos sinh and cosh are defined using their power series expansion. Those interested in the p-adic version of the theory of analytic manifolds usually called rigid geometry have a completely different set of concerns which dominate for example Non-Archimedean Analysis by Bosch. They give real R or p-adic Q p number fields where p is any prime number with corresponding p-adic norm x p which is non-Archimedean.
Developed over a century ago p-adic numbers have become an essential setting in which to investigate questions about rational numbers that go back millennia. The real analysis counterparts. The p -adic numbers are not as well known as the others but they play a fundamental role in number theory and in other parts of mathematics capturing information related to a chosen prime number p.
For example this is how you write 11 in the 3-adics. Mathematicians had noticed in the 1970s that many problems concerning p-adic numbers become easier if you expand the p-adic numbers by creating an infinite tower of number systems in which each one wraps around the one below it p times with the p-adic numbers at the bottom of the tower. It allows addition subtraction multiplication and division of p-adic numbers written in Hensel expansion.
PREPRINTS Heights and Tamagawa numbers of motives preprint availablehere. Nemo is a computer algebra package for the Julia programming language maintained byWilliam Hart Tommy Hofmann Claus Fieker and Fredrik Johansson with additional code byOleksandr Motsak and othercontributors. This formalization which has been verified in the Coq proof assistant provides an approach to the p-adic numbers in constructive algebra and analysis.
Value- int rem self. There is an adelic formula p x p 1 valid for rational xwhich expresses the real norm x in terms of p-adic ones. The p-adic numbers are based in modular arithmetic which is a method of counting that loops back on itself like a clock.
Mathematicians write p-adic numbers based on the frequency with which each power of p appears in the numbers base p expansion. Sum of two p-adic numbers def __init__ self p arg1 arg2. Introduction Fix pa prime number and Q p an algebraic closure of the eld of p-adic numbers Q p.
Each a k for k2fnn1n2gis known as a p-adic digit. Pros of symmetrization for 3-adic numbers are just the same. Numerator ModP self.
If Fis a eld which is a nite extension of Q. In this article we present a package that does p-adic calculations using Mathematica. Despite the fact that p-adic expansions are by de nition in nite they possess an important property making the de nition of Z p concrete and precise.
The size of a p-adic number is determined by the prevalence of p in its prime factorization. Functional Programming with Regular Coinductive Types. The goal of this paper is to report on a formalization of the p-adic numbers in the setting of the second authors univalent foundations program.
P-Adicization ProgramTGD as a Generalized Number Theory II. At the top of this infinite tower is the ultimate wraparound space a fractal object that is the simplest example of the. This she points out is different from real analysis and again commendably she almost always takes care to let us know the differences between the results of p-adic vs.
All the p-adic numbers are obtained by multiplying p-adic integers by p-k that is by shifting the sequences thus we got the representation for all 3-adic numbers not only integer ones. Simplicity of negation no curries at multiplication table. So given a p-adic metric on mathbb Q we have that Q embeds in the completion.
Tamgawa number conjecture for a p-adic family of F-crystals preprint availablehere.

I Mentioned To A Friend Of Mine That I Thought Learning Category Theory Might Be Useful For Computer Science And He Dismissed Category Theory Theories Category
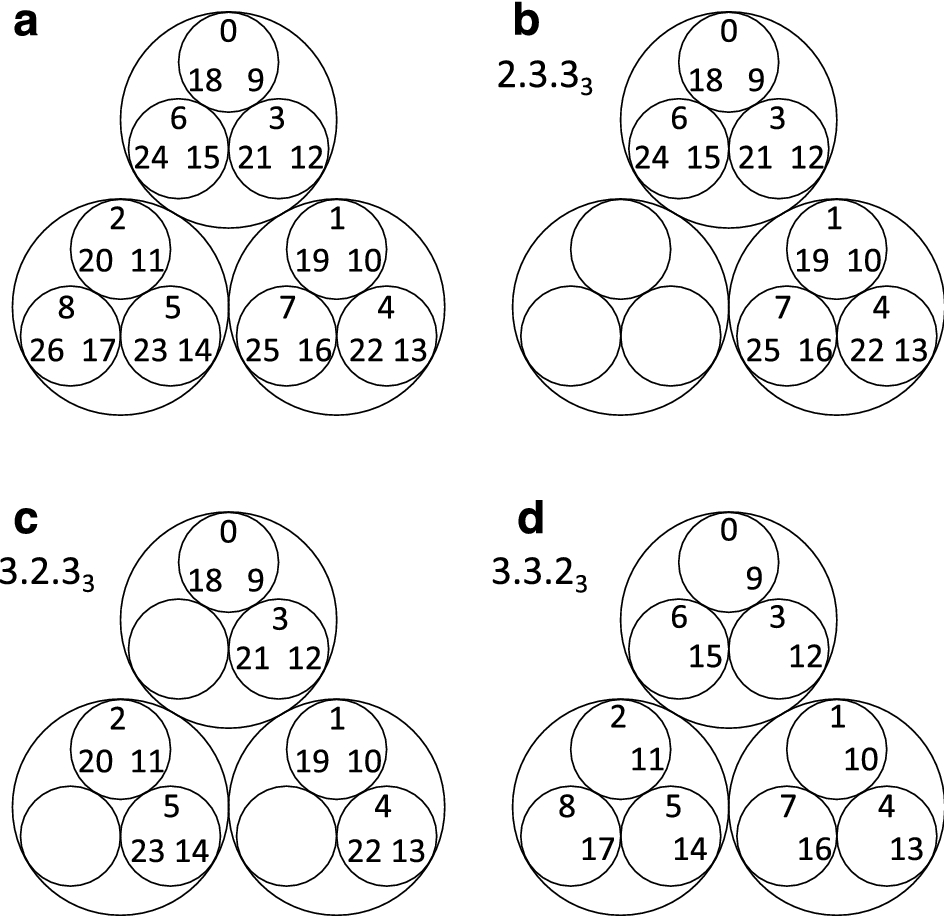
P Adic Numbers Encode Complex Networks Scientific Reports
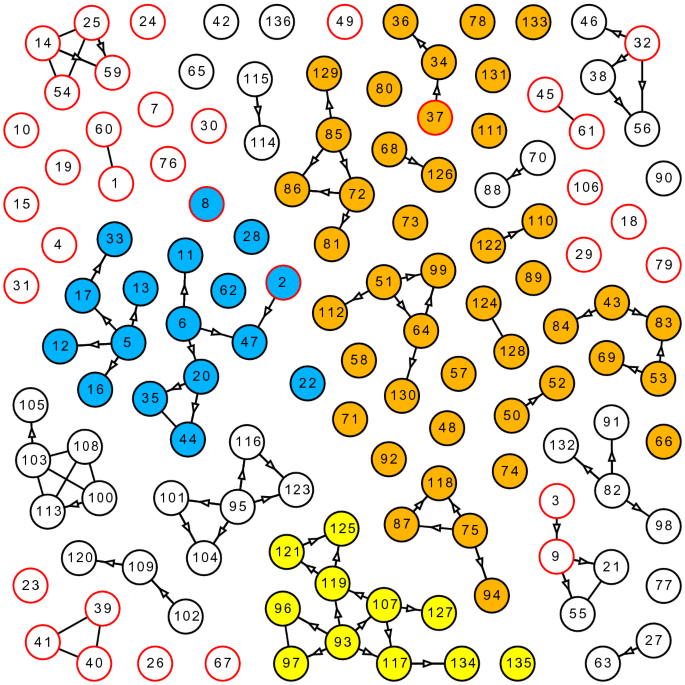
P Adic Numbers Encode Complex Networks Scientific Reports

Comment Below And Happy Birthday To Constructive Geometry Students Memes Math Funny Ahah Lmao Mathematics Math Memes Student Memes Memes

Type Theory And Homotopy Theory Theoretical Computer Science Type Theory Mathematics

P Adic Mathematics And Theoretical Biology Sciencedirect

Theory Of Computation Wikipedia The Free Encyclopedia Theory Of Computation Theoretical Computer Science Theories

Pin By Par Olanders On Hochu Math Books Science Textbook Physics And Mathematics

Example Of A Non Deterministic Finite State Automata Automata Mathematics Algorithm
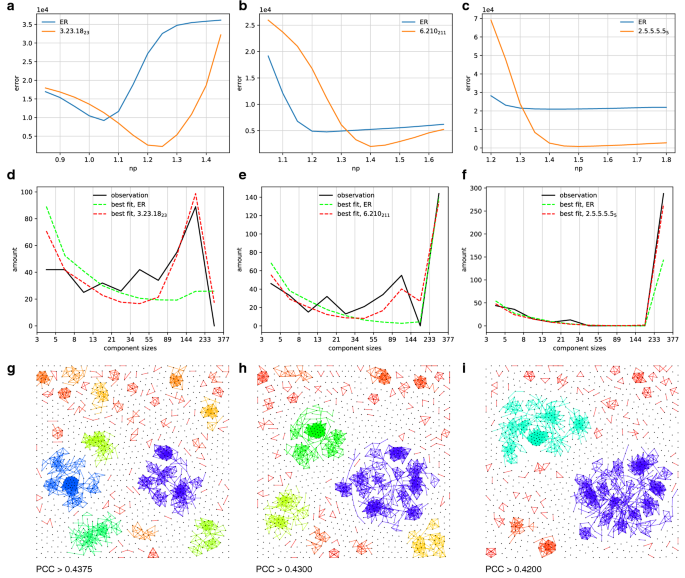
P Adic Numbers Encode Complex Networks Scientific Reports


Posting Komentar untuk "Programming P-adic Numbers"